Visualizing GJK in 3D
Skip ahead to the visualization.
Collision detection is perhaps one of the most ubiquitous features of any game engine. Surely we can make a game which doesn't need any type of collision detection whatsoever, however most games do need to detect whether an object has come into contact with another. Detecting collisions is to interactivity what sugar is to coffee. You can drink it without it, but having it just makes it so much better.
Now, I don't actually mind if you don't like sugar in your coffee. But I do care about how a seemingly complex task like checking for collisions for all 3D objects in a scene of a game running at 60 FPS can possibly be achieved. Luckily, a lot of people have concerned themselves with finding exactly that answer.
A Fast Procedure for Computing the Distance Between Complex Objects in Three-Dimensional Space is a paper[1] on the field of robotics and automation by Gilbert, Johnson and Keerthi (or GJK for short). In it, the authors describe an efficient algorithm for computing the Euclidean distance between a pair of convex set of points.
Most people who learn about GJK soon come to face the general consensus that the original paper is, in fact, very mathematically dense -- almost unnecessarily so. When it comes to the algorithm itself and its possible optimizations, many people have succeeded in explaining it in a much less abstract fashion.
If you are not yet familiar with the algorithm, I would highly encourage you to check references [2] and [3] before continuing, as my intent with this post is to provide you with a visualization tool for the algorithm's 3D case. I will not attempt to fully explain the algorithm, as the references already do a fantastic job at that.
From this point forward, I will assume that you are familiar with the algorithm, so let's just recap:
For any two sets of points (eg. objects) in euclidean space, we can compute the Minkowski difference between all the points in object A with all the points in object B, which will result in a shape that is the combination of the two objects.
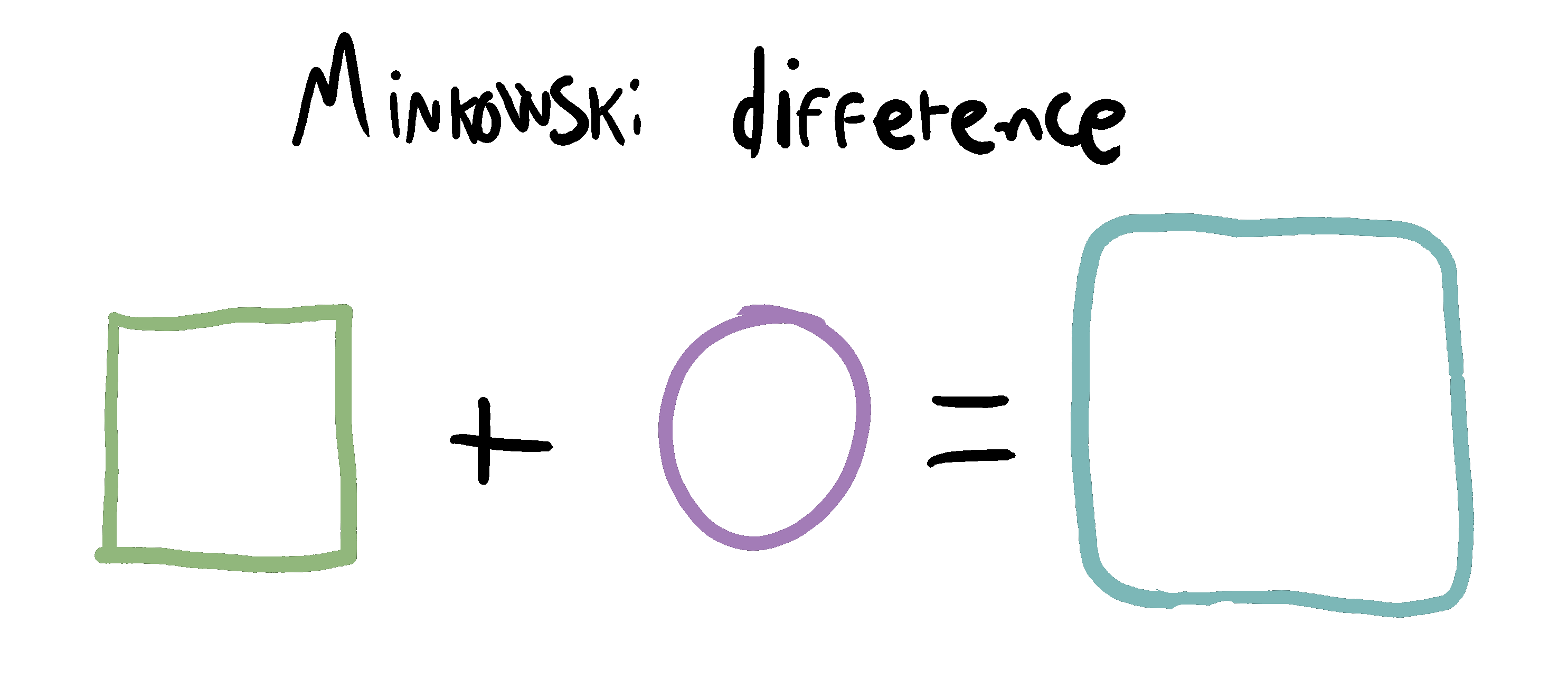
A nice property of the Minkowski difference is that if (and only if) the objects are intersecting one another in Euclidean space, their Minkowski space equivalent will contain the origin.
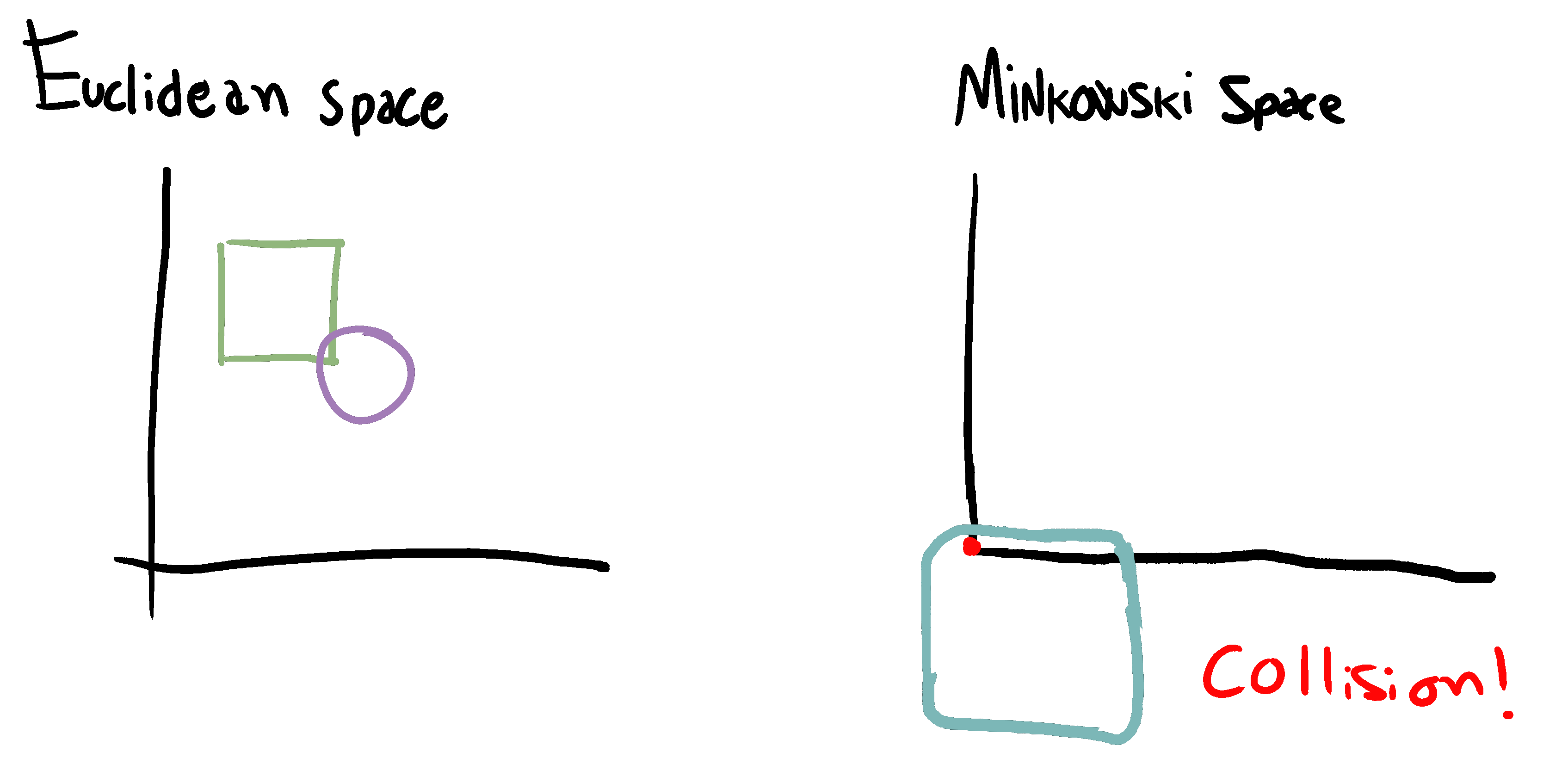
This property provides a reliable way to check if two convex objects of any complexity are intersecting one another, however building the whole Minkowski difference for every pair of objects every physics frame would be infeasible to say the least. That's why we are concerned in gathering the minimum amount of information to check whether the origin of the Minkowski space is contained in the difference or not. Enter the simplex.
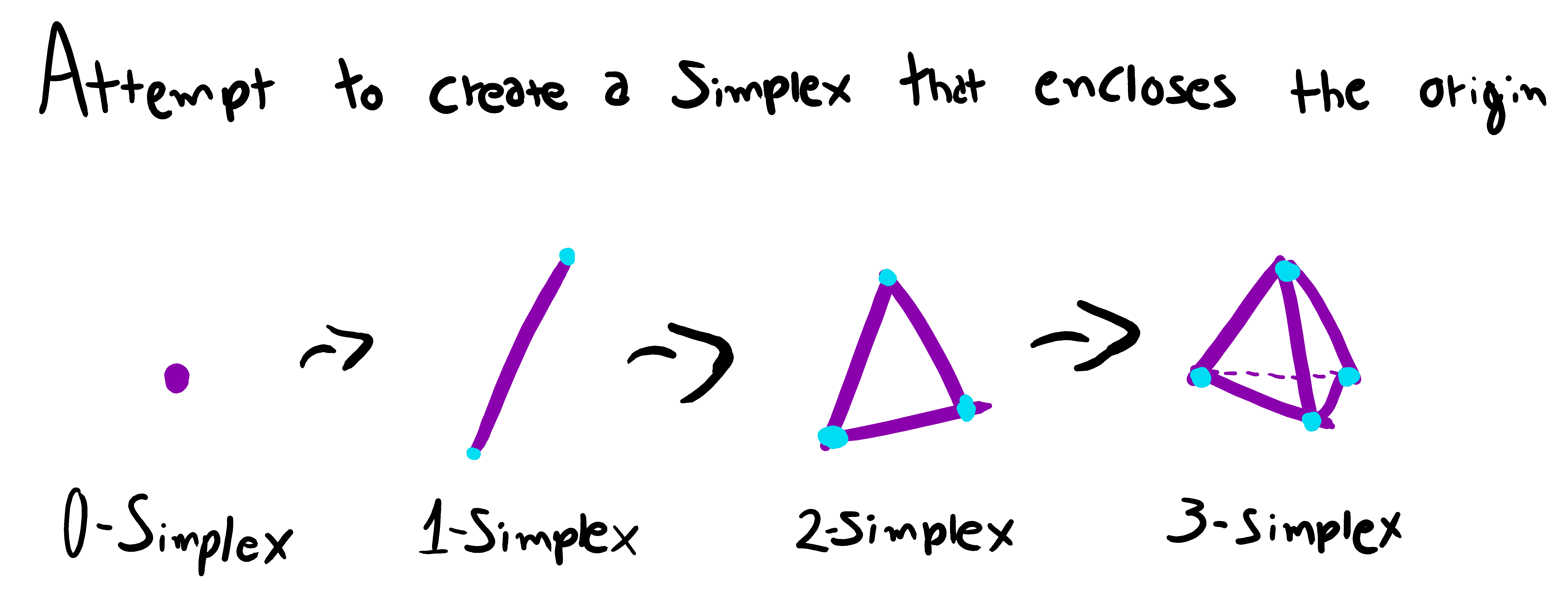
The algorithm (and its optimizations) intelligently searches only in directions that could possibly be useful for achieving this goal. The process is in fact very efficient and can be used as a reliable collision detection method.
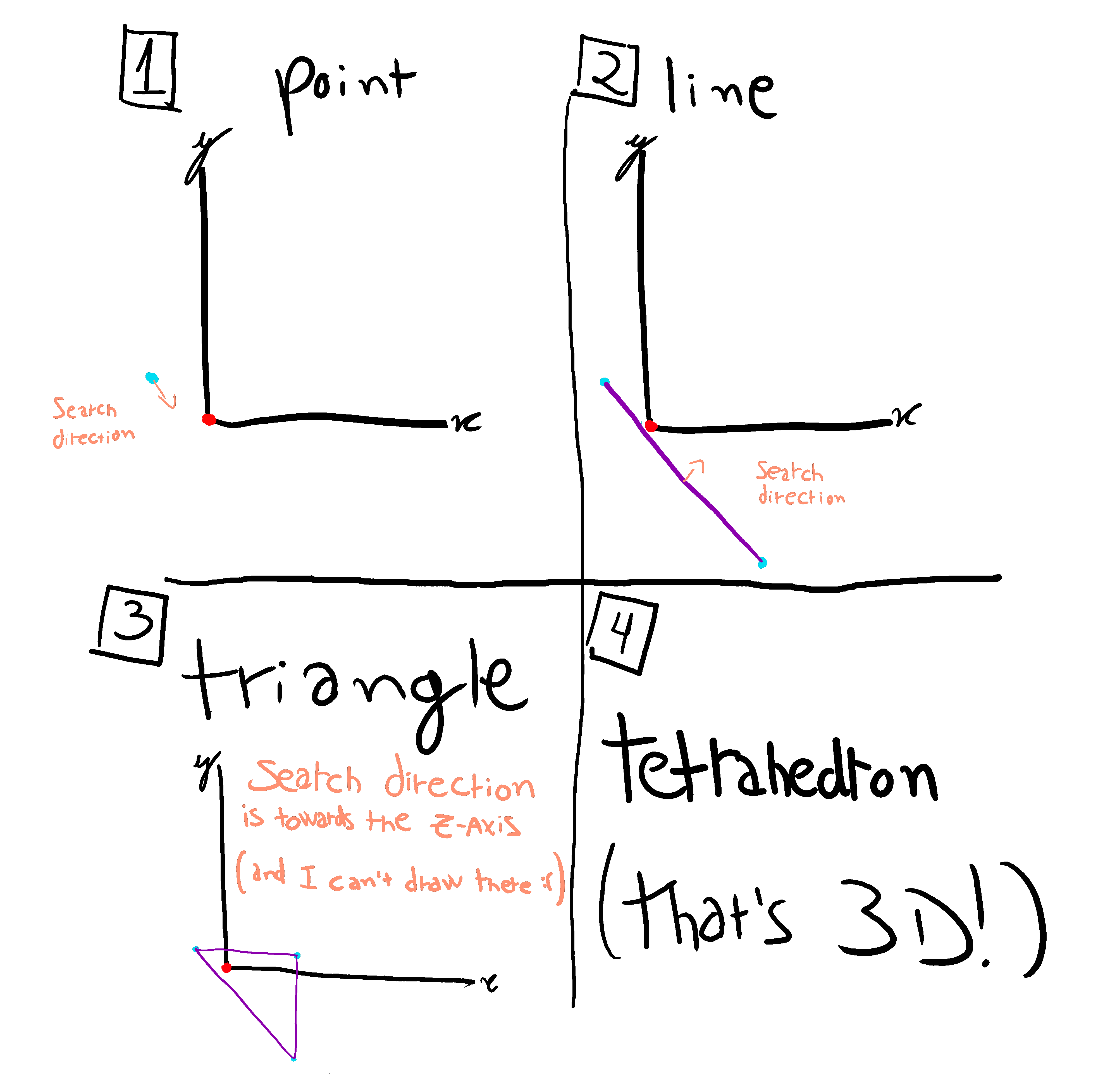
I'm a firm believer that good visualization tools are fundamental to get a proper understanding of an algorithm or a mathematical concept, and even though there are a quite a few resources out there about GJK, most of them reserve themselves to building the reader's intuition up to 2D, with no real way of visualizing how the construction of the 4-simplex for the 3D case would look like.
The tool below shows the Euclidean space representation of two objects, which can be translated around freely, and below it, the Minkowski space representation of their difference. Once the build simplex button is clicked, the tool will attempt to construct a 4-simplex to enclose the origin, step-by-step. The support points in the convex hull and the next search direction are also indicated between each step. The camera can be moved and zoomed around with the mouse in both spaces.
WebGL visualization:
Euclidean space
Building simplex...
Minkowski space
Hopefully some of you out there will find this useful!
Thanks for reading! Have a wonderful day.
References:
- Gilbert, Johnson, Keerthi - A Fast Procedure for Computing the Distance Between Complex Objects in Three-Dimensional Space - 1988 [Paper]
- Casey Muratori - Implementing GJK - 2006 [Online lecture]
- Erin Catto - Computing Distance - GDC 2010 [Presentation]